farad per metre

SI coherent derived unit whose name and symbol includes an SI coherent derived unit with a special name and symbol

Name	Symbol	Quantity	Base units
farad per metre	F/m	permittivity	kg⁻¹ m⁻³ s⁴ A²
The farad per metre, symbol F/m, is the SI coherent derived unit of electric permittivity. One farad per metre is equal to the permittivity of an electrical insulator that produces an electric displacement field of one coulomb per square metre when an electric field of one volt per metre is applied to it.
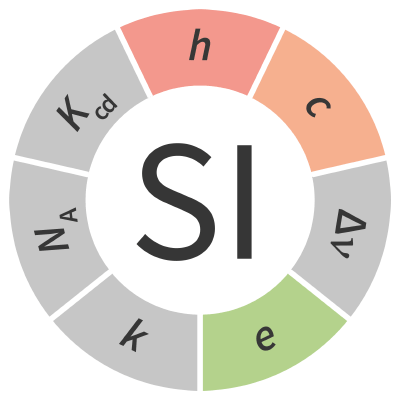
Definition			h^-1 c^-1 e²
$1 \mspace{4mu} \text{F} / \text{m} \mspace{6mu} = \dfrac{(6.626 \mspace{4mu} 070 \mspace{4mu} 15 \times 10^{-34})(299 \mspace{4mu} 792 \mspace{4mu} 458)}{(1.602 \mspace{4mu} 176 \mspace{4mu} 634 \times 10^{-19})^2} \mspace{6mu} \dfrac{e^2}{h \mspace{4mu} c}\\ \\ \\ 1 \mspace{4mu} \text{F} / \text{m} \mspace{6mu} \approx 7.738 \mspace{4mu} 484 \mspace{4mu} 996 \mspace{4mu} 105 \mspace{4mu} 633 \mspace{4mu} 022 \times10^{12} \mspace{6mu} h^{-1} \mspace{4mu} c^{-1} \mspace{4mu} e^2$

Permittivity

In electromagnetism, an electrical insulator that can be polarised by an applied electric field is called a dielectric. Permittivity is a measure of the amount of electric polarisation that is produced in a dielectric material in response to an applied electric field.

When an electric field is applied to a material, the resulting electric displacement field, D, is directly proportional to the strength of the applied electric field, E, and the permittivity, ε, of the material.

Using SI coherent units,

$\mathbf{D} = \varepsilon \mspace{2mu} \mathbf{E} \\ \\ \varepsilon = \dfrac{\mathbf{D}}{\mathbf{E}}$

where:

D is the electric displacement field in coulombs per square metre, symbol C m^-2,
E is the strength of the applied electric field in volts per metre, symbol V m^-1,
ε is the electric permittivity in farads per metre, symbol F m^-1.

Electric permittivity, ε, is analogous to magnetic permeability, μ.

Electric constant

The electric constant, ε₀, also known as the permittivity of free space, or vacuum electric permittivity, is the value of the permittivity of vacuum.

From Maxwell’s equations, it is possible to derive an expression for the speed of light, c, in terms of the electric constant, ε₀, and the magnetic constant, μ₀:

$c = \dfrac{1}{ \sqrt{{\varepsilon}_0 \mspace{2mu} {\mu}_0}}$

It follows that ε₀ can be defined as follows:

${\varepsilon}_0 = \dfrac{1}{{\mu}_0 \mspace{2mu} c^2}$

where:

ε₀ is the electric permittivity of vacuum in farads per metre, symbol F m^-1,
μ₀ is the magnetic permeability of vacuum in henries per metre, symbol H m^-1.
c is the speed of light in vacuum in metres per second, symbol m s^-1,

Prior to 2019, the ampere was defined such that the value of the magnetic constant, μ₀, or magnetic permeability of vacuum, was exactly equal to 4π × 10⁻⁷ H m^-1. This implied an exact value for the electric constant, ε₀:

${\varepsilon}_0 = \dfrac{1}{(4 \pi \times 10^{-7} \mspace{4mu} \text{H} \mspace{4mu} \text{m}^{-1}) \mspace{4mu} c^2}$

As a consequence of the 2019 redefinition of the ampere, the electric constant is no longer defined with an exact numeric value. Its definitive value now depends on the measured value of the fine-structure constant. However, its approximate value can still be calculated as follows:

${\varepsilon}_0 \approx \dfrac{1}{(4 \pi \times 10^{-7} \mspace{4mu} \text{H} \mspace{4mu} \text{m}^{-1}) (299 \mspace{4mu} 792 \mspace{4mu} 458 \mspace{4mu} \text{m} \mspace{4mu} \text{s}^{-1})^2}\\ \\ \\ {\varepsilon}_0 \approx 8.854 \mspace{4mu} 187 \mspace{4mu} 817 \mspace{4mu} 620 \times 10^{-12} \mspace{4mu} \text{F} \mspace{4mu} \text{m}^{-1}$

Fine-structure constant

The fine-structure constant is a fundamental physical constant which quantifies the strength of the electromagnetic interaction between elementary charged particles. The fine-structure constant, α, is dimensionless and can be defined in terms of the electric constant or the magnetic constant as follows:

Using SI coherent units,

$\alpha \mspace{6mu} = \mspace{6mu} \dfrac{1}{2 \mspace{2mu} {\varepsilon}_0} \mspace{2mu} \dfrac{e^2}{h \mspace{2mu} c} \mspace{6mu} = \mspace{6mu} \dfrac{{\mu}_0}{2} \mspace{2mu} \dfrac{c \mspace{2mu} e^2}{h}$

where:

ε₀ is the electric constant in farads per metre, symbol F m^-1,
μ₀ is the magnetic constant in henries per metre, symbol H m^-1,
h is the Planck constant in joule seconds, symbol J s,
c is the speed of light in vacuum in metres per second, symbol m s^-1,
e is the elementary charge in coulombs, symbol C.

It follows that the electric constant, ε₀, can be defined in terms of the fine-structure constant, α:

${\varepsilon}_0 \mspace{4mu} = \mspace{4mu} \dfrac{1}{2 \mspace{2mu} \alpha} \mspace{2mu} \dfrac{e^2}{h \mspace{2mu} c}$

In the SI, h, c and e are all defined with exact numeric values, which means that the value of the electric constant, ε₀, depends on only one measured value – the fine-structure constant, α. The measured numerical value of α is 0.007 297 352 564 3(11).

Thus the value of the electric constant, ε₀, can be calculated as follows:

${\varepsilon}_0 = \dfrac{(1.602 \mspace{4mu} 176 \mspace{4mu} 634 \times 10^{-19} \mspace{4mu} \text{C})^2}{(2 \times 0.007 \mspace{4mu} 297 \mspace{4mu} 352 \mspace{4mu} 564 \mspace{4mu} 3(11))(6.626 \mspace{4mu} 070 \mspace{4mu} 15 \times 10^{-34} \mspace{4mu} \text{J} \mspace{4mu} \text{s})(299 \mspace{4mu} 792 \mspace{4mu} 458 \mspace{4mu} \text{m} \mspace{4mu} \text{s}^{-1})}\\ \\ \\ {\varepsilon}_0 = 8.854 \mspace{4mu} 187 \mspace{4mu} 818 \mspace{4mu} 8(14) \times 10^{-12} \mspace{4mu} \text{F} \mspace{4mu} \text{m}^{-1}$