SI defining constants

All units in the International System of Units (SI) are defined by the seven constants listed in Table 1. These constants are based on unchanging properties of nature. In the SI, each of the seven defining constants has a fixed exact numerical value. The defining constants can be expressed using SI coherent derived units, or with a combination of SI base units.

The defining constants have been chosen such that, when taken together, their units cover all of the units of the SI. Any SI unit is a product of powers of these seven constants and a dimensionless factor.

Table 1

Name	Symbol	Base units
Planck constant	h	kg m2 s−1
speed of light in vacuum	c	m s−1
caesium frequency	ΔνCs	s−1
elementary charge	e	s A
Boltzmann constant	k	kg m2 s-2 K-1
Avogadro constant	NA	mol-1
luminous efficacy of monochromatic radiation of frequency 540 × 1012 Hz	Kcd	kg−1 m−2 s3 cd

These definitions specify the exact numerical value of each constant when its value is expressed in the corresponding SI unit. By fixing the exact numerical value the unit becomes defined, since the product of the numerical value {Q} and the unit [Q] has to equal the value Q of the constant, which is invariant: Q = {Q} [Q].

SI defining constants expressed in terms of base units

From Table 1, it can be seen that each defining constant can be expressed as the product of powers of the SI base units:

kg^α m^β s^γ A^δ K^ε mol^ζ cd^η

Table 2

								Base units
	1	2	-1	0	0	0	0	kg m2 s−1
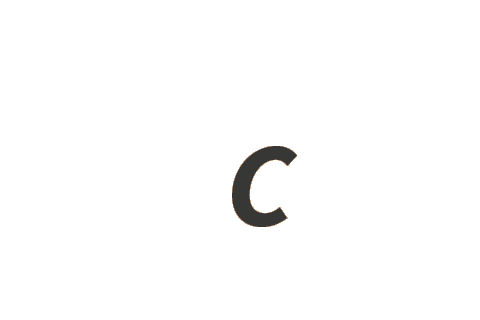	0	1	-1	0	0	0	0	m s−1
	0	0	-1	0	0	0	0	s−1
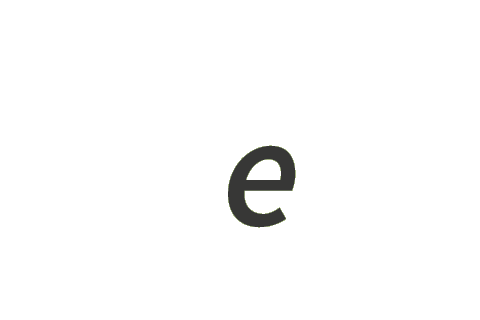	0	0	1	1	0	0	0	s A
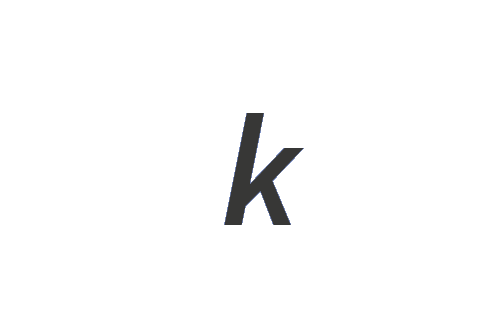	1	2	-2	0	-1	0	0	kg m2 s−2 K−1
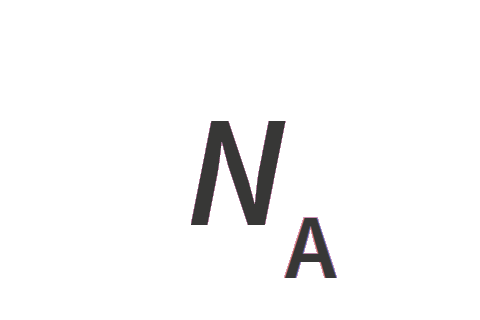	0	0	0	0	0	-1	0	mol−1
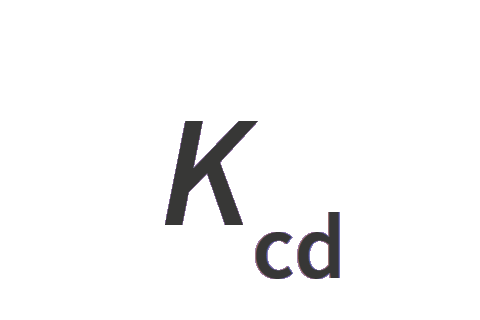	-1	-2	3	0	0	0	1	kg−1 m−2 s3 cd

The exponents required for each defining constant are presented in rows in Table 2. For example, the exponents used for the Planck constant, h, are (1, 2, −1, 0, 0, 0, 0), giving the coherent unit kg¹ m² s⁻¹ A⁰ K⁰ mol⁰ cd⁰. Exponent values of zero result in a factor of one, and can be discarded, so in this example the coherent unit is kg m² s⁻¹.

SI base units expressed in terms of defining constants

The seven SI base units can be defined in terms of the seven SI defining constants. For some base units, it is straight forward to see how to express them in terms of defining constants.

For example, given that Δν_Cs = 9 192 631 770 s^-1, it follows that 1 s = 9 192 631 770 Δν_Cs^-1.

However, for base units such as the kilogram, which is defined by 3 different constants, matrix mathematics makes the task more manageable.

The exponent values in Table 2 constitute a 7 × 7 matrix. Inverting this matrix gives the exponents required to express each SI base unit in terms of the product of powers of the defining constants:

h^α′ c^β′ Δν_Cs^γ′ e^δ′ k^ε′ N_A^ζ′ K_cd^η′

Table 3

								Defining constants
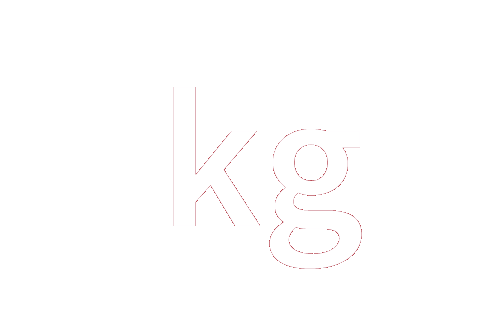	1	-2	1	0	0	0	0	h c−2 ΔνCs
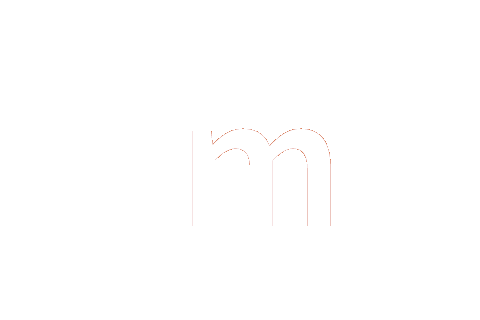	0	1	-1	0	0	0	0	c ΔνCs−1
	0	0	-1	0	0	0	0	ΔνCs−1
	0	0	1	1	0	0	0	ΔνCs e
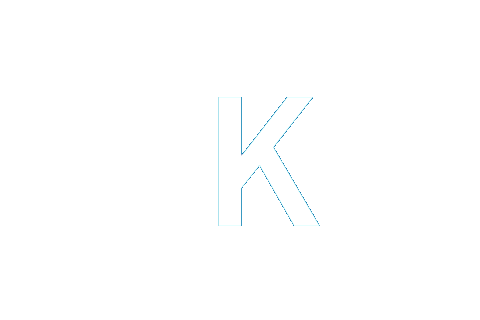	1	0	1	0	-1	0	0	h ΔνCs k−1
	0	0	0	0	0	-1	0	NA−1
	1	0	2	0	0	0	1	h ΔνCs2 Kcd

The exponents required for each SI base unit are presented in rows in Table 3. For example, the exponents used for the kilogram, kg, are (1, −2, 1, 0, 0, 0, 0), giving the combined constant h¹ c⁻² Δν_Cs¹ e⁰ k⁰ N_A⁰ K_cd⁰. Exponent values of zero result in a factor of one, and can be discarded, so in this example the combined constant is h c⁻² Δν_Cs.

Scaling factors for the SI base unit definitions

Table 3 excludes scaling factors. The calculations to derive the exact scaling factor for each SI base unit definition are shown below. For each base unit, substituting the values from Table 1 into the left side of the equation, which is a combination of SI defining constants, gives us the right side, which is the value of the combination in the SI.

SI base units expressed in terms of defining constants

Table 4 presents the seven SI base units as defined by products of powers of the SI defining constants.

Table 4

Name	Symbol	Defining constants
kilogram	kg	h c−2 ΔνCs
metre	m	c ΔνCs−1
second	s	ΔνCs−1
ampere	A	ΔνCs e
kelvin	K	h ΔνCs k−1
mole	mol	NA−1
candela	cd	h ΔνCs2 Kcd

Since all seven base units of the SI can be defined in terms of the seven defining constants, it follows that all other SI units can also be defined in terms of the seven defining constants.

SI derived units expressed in terms of defining constants

All SI coherent units can be expressed as products of powers of the seven SI base units:

kg^α m^β s^γ A^δ K^ε mol^ζ cd^η

where α, β, γ, δ, ε, ζ, η represent the exponents of their respective base units.

Table 5 shows how any SI coherent unit can also be expressed in terms of products of powers of the seven SI defining constants.

The values presented in each column are the exponent values of the defining constants used to express each base unit factor of a coherent unit.

To obtain an expression for the SI coherent unit as a whole, the defining constants for each base unit factor are multiplied together. This is done by adding the exponents in each row. The results of which are presented in the rightmost column.

Table 5

								Defining constants
	α	0	0	0	ε	0	η	h(α+ε+η)
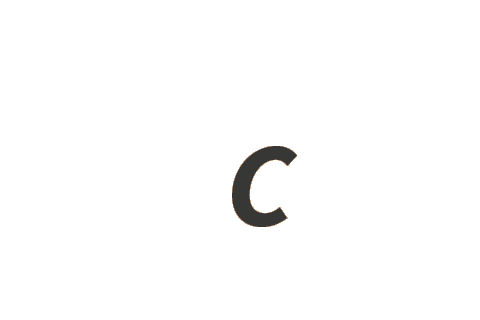	-2α	β	0	0	0	0	0	c(‑2α+β)
	α	-β	-γ	δ	ε	0	2η	ΔνCs(α‑β‑γ+δ+ε+2η)
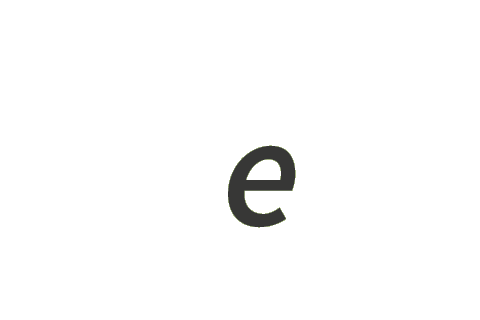	0	0	0	δ	0	0	0	eδ
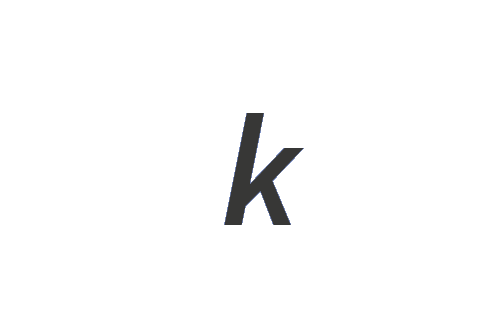	0	0	0	0	-ε	0	0	k-ε
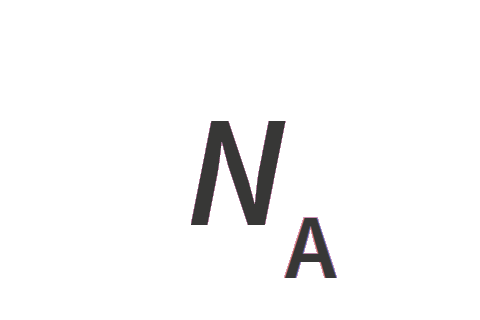	0	0	0	0	0	-ζ	0	NA-ζ
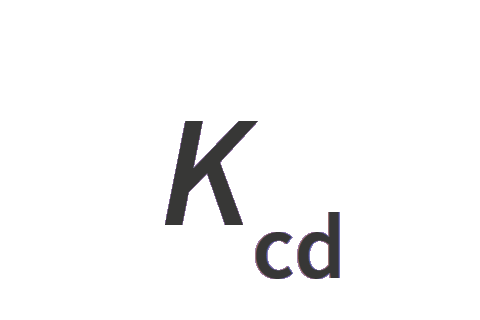	0	0	0	0	0	0	η	Kcdη

The desired expression is obtained by multiplying together all the values in the rightmost column:

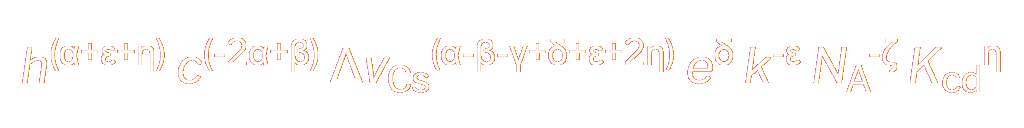This expression can be used to obtain the definition for any SI coherent unit expressed in the form kg^α m^β s^γ A^δ K^ε mol^ζ cd^η .

For example, the ohm is equal to kg m² s^-3 A^-2 when expressed in terms of SI base units, which gives values of (1, 2, -3, -2, 0, 0, 0) for (α, β, γ, δ, ε, ζ, η). Substituting these values in the defining constants expression gives the following:

h^(1+0+0) c^(-2+2) Δν_Cs^{(1-2+3-2+0+0)} e^-2 k⁰ N_A⁰ K_cd⁰

Factors of the resulting expression that have exponents of zero are equal to one, and can be discarded, which in this example leaves:

h e^-2

The necessary dimensionless scaling factor is calculated by copying the above result and substituting the respective numeric value of each defining constant. This value is then inverted, by negating the exponents, to produce the required scaling factor. Thus:

1 Ω = (6.626 070 15 × 10⁻³⁴)⁻¹ (1.602 176 634 × 10⁻¹⁹)² h e^-2
 
1 Ω ≈ 3.874 045 864 931 825 323 × 10⁻⁵ h e^-2

A similar exercise can be carried out for any given SI coherent unit.

All SI coherent derived units can be defined either from the SI base units or more directly from the SI defining constants. The distinction between SI base units and SI derived units remains useful, but is not essential.